求小于n的质数的个数——埃拉托斯特尼筛法

Algorithms

问题描述

给定一个非负数n，求小于n的质数的个数。

算法描述

在本题中，我们采用埃拉托斯特尼筛法，详细列出算法如下：

  1. 从2开始遍历到根号n；
  2. 先找到第一个质数2，然后将其所有的倍数全部标记出来；
  3. 然后到下一个质数3，标记其所有倍数，依次类推，直到根号n；
  4. 此时数组中未被标记的数字就是质数。

效果图如下：

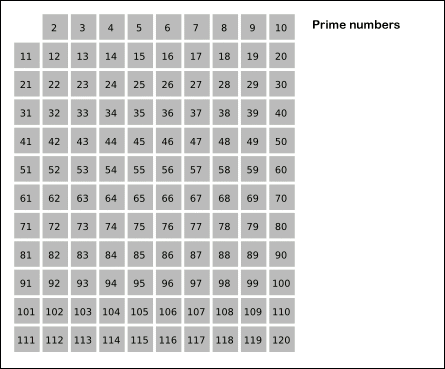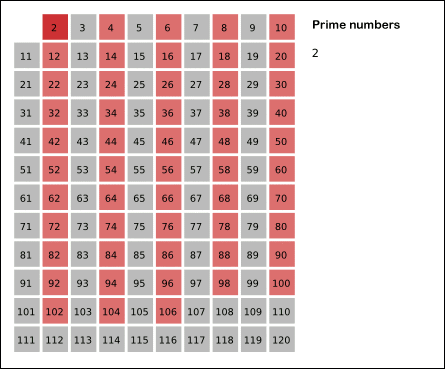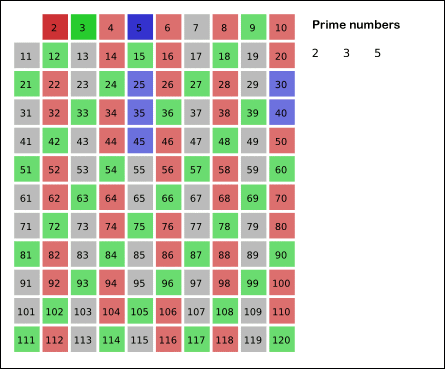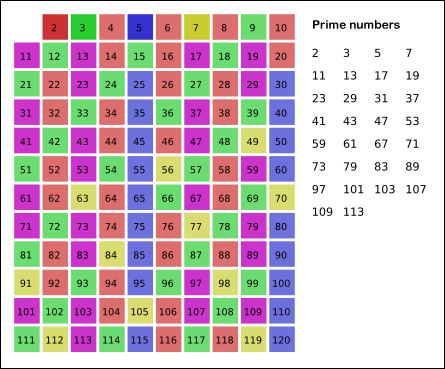
Sieve_of_Eratosthenes_animation

下面给出ruby和python代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
!#/usr/bin/ruby
# @param {Integer} n
# @return {Integer}
def count_primes(n)
  return 0 if n < 2

  mark = [true] * n
  mark[0], mark[1] = false, false

  2.upto(Math.sqrt(n)) do |i|
    if mark[i]
      p = i ** 2
      while p < n
        mark[p] = false
        p += x
      end
    end
  end
  mark.count(true)
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
!#/usr/bin/python
def _odd_iter():
    n=1
    while True:
        n = n + 2
        yield n

def _not_divisible(n):
    return lambda x : x % n > 0

def primes():
    yield 2
    it = _odd_iter()
    while True:
        n=next(it)
        yield n
        it = filter(_not_divisible(n), it)

for n in primes():
    if n < 1000:
        print(n)
    else:
        break