Java源码解析 —— TreeMap

YXiao's Blog

2018-04-09

Java › Source Code

前言

TreeMap是基于红黑树结构实现的一种Map，要分析TreeMap的实现首先就要对红黑树有所了解。

构造图如下:
蓝色线条：继承
绿色线条：接口实现

treemap

红黑树简介

TreeMap底层是基于红黑树（Red-Black tree）实现，所以在学习TreeMap之前我们先来了解下红黑树。

红黑树又称红-黑二叉树，它首先是一颗二叉树，它具有二叉树所有的特性。同时红黑树更是一棵自平衡的排序二叉树。

我们知道一颗基本的二叉排序树他们都需要满足一个基本性质–即树中的任何节点的值大于它的左子节点，且小于它的右子节点。按照这个基本性质使得树的检索效率大大提高。我们知道在生成二叉排序树的过程是非常容易失衡的，最坏的情况就是一边倒（只有右/左子树），这样势必会导致二叉树的检索效率大大降低（O(n)），所以为了维持二叉排序树的平衡，大牛们提出了各种实现的算法，如：AVL，SBT，伸展树，TREAP，红黑树等等。

平衡二叉树必须具备如下特性：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。也就是说该二叉树的任何一个等等子节点，其左右子树的高度都相近。

红黑树顾名思义就是节点是红色或者黑色的平衡二叉树，它通过颜色的约束来维持着二叉树的平衡。对于一棵有效的红黑树而言我们必须增加如下规则：

每个节点都只能是红色或者黑色
根节点是黑色
每个叶节点（NIL节点，空节点）是黑色的
如果一个结点是红的，则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点
从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点

红黑树示意图如下：

red-black_tree

但是在在添加或删除节点后，红黑树就发生了变化，可能不再满足上面的5个特性，为了保持红黑树的以上特性，就有了三个动作：左旋、右旋、着色。

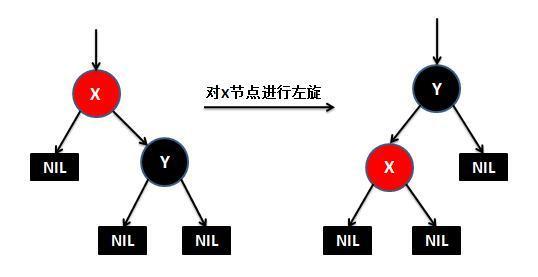
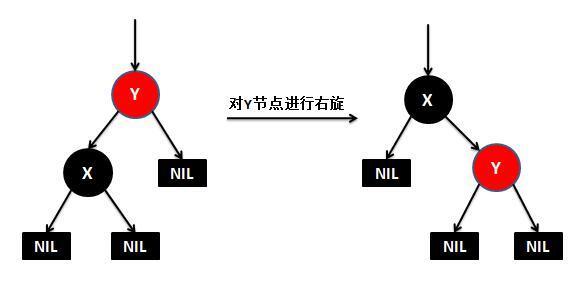
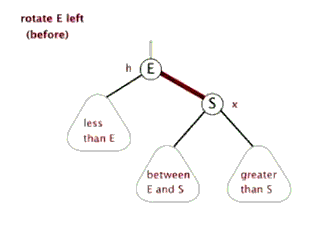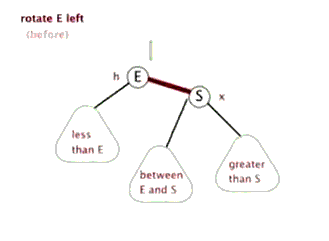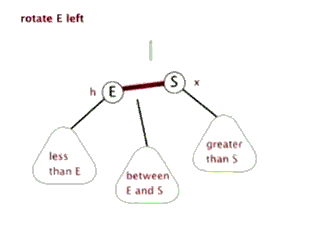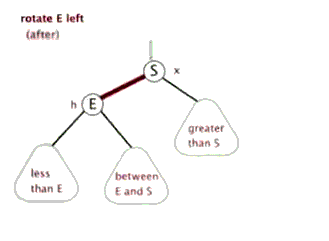
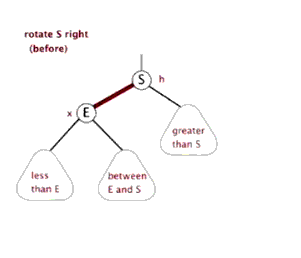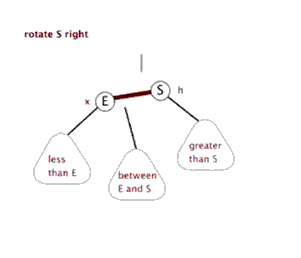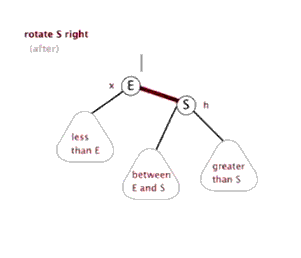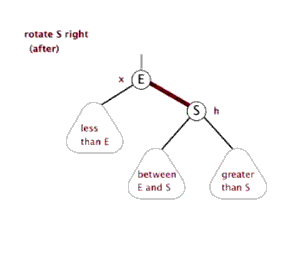
下面来看下什么是红黑树的左旋和右旋：

rotate_left

对x进行左旋，意味着”将x变成一个左节点”。

rotate_right

对y进行右旋，意味着”将y变成一个右节点”。

如果还是没看明白，下面找了两张左旋和右旋的动态图:

rotate_left

rotate_right

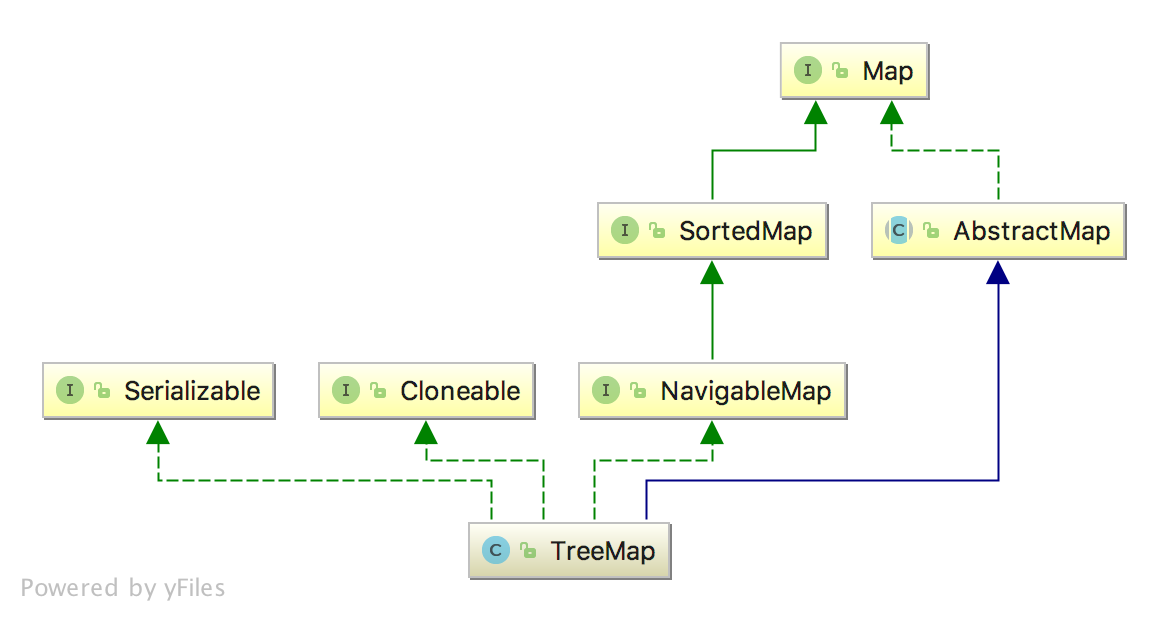
TreeMap简介

定义

1
2
3

public class TreeMap<K,V>
    extends AbstractMap<K,V>
    implements NavigableMap<K,V>, Cloneable, java.io.Serializable

TreeMap 是一个有序的key-value集合，它是通过红黑树实现的。
TreeMap 继承于AbstractMap，所以它是一个Map，即一个key-value集合。
TreeMap 实现了NavigableMap接口，意味着它支持一系列的导航方法。比如返回有序的key集合。
TreeMap 实现了Cloneable接口，意味着它能被克隆。
TreeMap 实现了java.io.Serializable接口，意味着它支持序列化。

TreeMap基于红黑树（Red-Black tree）实现。该映射根据其键的自然顺序进行排序，或者根据创建映射时提供的Comparator进行排序，具体取决于使用的构造方法。

TreeMap的基本操作containsKey、get、put和remove的时间复杂度是log(n)。

另外，TreeMap是非同步的。它的iterator方法返回的迭代器是fail-fast的。

TreeMap属性

// 比较器
private final Comparator<? super K> comparator;

// 红黑树根节点
private transient Entry<K,V> root;

// 集合元素数量
private transient int size = 0;

// "fail-fast"集合修改记录
private transient int modCount = 0;

TreeMap的本质是R-B Tree(红黑树)，它包含几个重要的成员变量：root, size, comparator。

root是红黑数的根节点。它是Entry类型，Entry是红黑数的节点，它包含了红黑数的6个基本组成成分：key(键)、value(值)、left(左孩子)、right(右孩子)、parent(父节点)、color(颜色)。Entry节点根据key进行排序，Entry节点包含的内容为value。
红黑数排序时，根据Entry中的key进行排序；Entry中的key比较大小是根据比较器comparator来进行判断的，默认按照key的自然顺序排序。
size是红黑数中节点的个数。

Entry是树的节点类，我们来看一下Entry的定义：

static final class Entry<K,V> implements Map.Entry<K,V> {
    K key;
    V value;
    // 左孩子节点
    Entry<K,V> left;
    // 右孩子节点
    Entry<K,V> right;
    // 父节点
    Entry<K,V> parent;
    // 红黑树用来表示节点颜色的属性，默认为黑色
    boolean color = BLACK;

    /**
     * 用key，value和父节点构造一个Entry，默认为黑色
     */
    Entry(K key, V value, Entry<K,V> parent) {
        this.key = key;
        this.value = value;
        this.parent = parent;
    }

    public K getKey() {
        return key;
    }

    public V getValue() {
        return value;
    }

    public V setValue(V value) {
        V oldValue = this.value;
        this.value = value;
        return oldValue;
    }

    public boolean equals(Object o) {
        if (!(o instanceof Map.Entry))
            return false;
        Map.Entry<?,?> e = (Map.Entry<?,?>)o;

        return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
    }

    public int hashCode() {
        int keyHash = (key==null ? 0 : key.hashCode());
        int valueHash = (value==null ? 0 : value.hashCode());
        return keyHash ^ valueHash;
    }

    public String toString() {
        return key + "=" + value;
    }
}

Entry类理解起来比较简单（因为我们前面看过很多的Entry类了），主要是定义了树的孩子和父亲节点引用，和红黑颜色属性，并对equals和hashCode进行重写，以利于比较是否相等。

TreeMap构造函数

/**
 * 默认构造方法，comparator为空，代表使用key的自然顺序来维持TreeMap的顺序，这里要求key必须实现Comparable接口
 */
public TreeMap() {
    comparator = null;
}

/**
 * 用指定的比较器构造一个TreeMap
 */
public TreeMap(Comparator<? super K> comparator) {
    this.comparator = comparator;
}

/**
 * 构造一个指定map的TreeMap，同样比较器comparator为空，使用key的自然顺序排序
 */
public TreeMap(Map<? extends K, ? extends V> m) {
    comparator = null;
    putAll(m);
}

/**
 * 构造一个指定SortedMap的TreeMap，根据SortedMap的比较器来来维持TreeMap的顺序
 */
public TreeMap(SortedMap<K, ? extends V> m) {
    comparator = m.comparator();
    try {
        buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
    } catch (java.io.IOException cannotHappen) {
    } catch (ClassNotFoundException cannotHappen) {
    }
}

从构造方法中可以看出，要创建一个红黑树实现的TreeMap必须要有一个用于比较大小的比较器，因为只有能够比较大小才能实现红黑树的左孩子 < 树根 < 右孩子的特点。

源码解析

红黑树的添加原理及TreeMap的put实现

将一个节点添加到红黑树中，通常需要下面几个步骤：

1.将红黑树当成一颗二叉查找树，将节点插入。
这一步比较简单，就上开始我们自己写的二叉查找树的操作一样，至于为什么可以这样插入，是因为红黑树本身就是一个二叉查找树。
2.将新插入的节点设置为红色。
有没有疑问，为什么新插入的节点一定要是红色的，因为新插入节点为红色，不会违背红黑规则第5条，少违背一条就少处理一种情况。
3.通过旋转和着色，使它恢复平衡，重新变成一颗符合规则的红黑树。
要想知道怎么样进行左旋和右旋，首先就要知道为什么要进行左旋和右旋。

我们来对比下红黑树的规则和新插入节点后的情况，看下新插入节点会违背哪些规则。

① 节点是红色或黑色。
这一点肯定是不会违背的了。
② 根节点是黑色。
这一点也不会违背了，如果是根节点，只需将根节点插入就好了，因为默认是黑色。
③ 每个叶节点（NIL节点，空节点）是黑色的。
这一点也不会违背的，我们插入的是非空的节点，不会影响空节点。
④ 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
这一点是有可能违背的，我们将新插入的节点都设置成红色，如果其父节点也是红色的话，那就产生冲突了。
⑤ 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
这一点也不会违背，因为我们将新插入的节点都设置成红色。

了解了红黑树左旋和右旋操作，以及新插入节点主要是可能会违背红黑树的规则④后，我们来分析下，添加新节点的过程有哪几种情况：

新插入节点为根节点。这种情况直接将新插入节点设置为根节点即可，无需进行后续的旋转和着色处理。
新插入节点的父节点是黑色。这种情况直接将新节点插入即可，不会违背规则④。
新插入节点的父节点是红色。这种情况会违背规则④，而这种情况又分为了以下几种，下面进行图解：

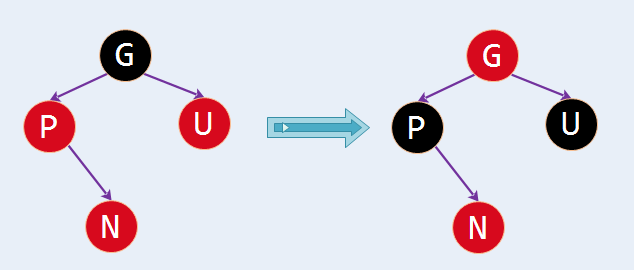
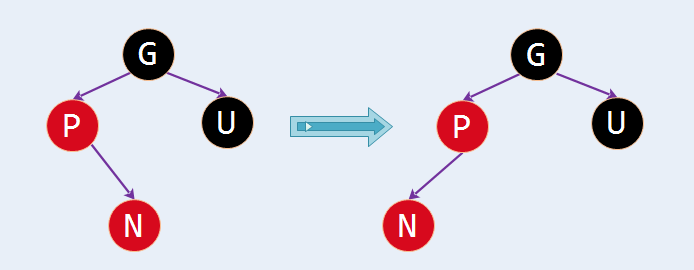
(1) 新插入节点N的父节点P和叔叔节点U都是红色。方法是：将祖父节点G设置为红色，父节点P和叔叔节点U设置为黑色，这时候就看似平衡了。但是，如果祖父节点G的父节点也是红色，这时候又违背规则④了，怎么办，方法是：将GPUN这一组看成一个新的节点，按照前面的方案递归；又但是根节点为红就违反规则②了，怎么办，方法是直接将根节点设置为黑色（两个连续黑色是没问题的）。

case1

(2) 新插入节点N的父节点P是红色，叔叔节点U是黑色或者缺少，且新节点N是P的右孩子。方法是：左旋父节点P。左旋后N和P角色互换，但是P和N还是连续的两个红色节点，还没有平衡，怎么办，看第三种情况。

case2

(3) 新插入节点N的父节点P是红色，叔叔节点U是黑色或者缺少，且新节点N是P的左孩子。方法是：右旋祖父节点G，然后将P设置为黑色，G设置为红色，达到平衡。此时父节点P是黑色，所以不用担心P的父节点是红色。

当然上面说的三种情况都是基于一个前提：新插入节点N的父节点P是祖父节点G的左孩子，如果P是G的右孩子又是什么情况呢？其实情况和上面是相似的，只需要调整左旋还是右旋，这里就不细说了。

下面看一下TreeMap的put实现：

public V put(K key, V value) {
    // 根节点
    Entry<K,V> t = root;
    // 如果根节点为空，则直接创建一个根节点，返回
    if (t == null) {
        compare(key, key); // type (and possibly null) check
        root = new Entry<K,V>(key, value, null);
        size = 1;
        modCount++;
        return null;
    }
    // 记录比较结果
    int cmp;
    Entry<K,V> parent;
    // split comparator and comparable paths
    // 当前使用的比较器
    Comparator<? super K> cpr = comparator ;
    // 如果比较器不为空，就是用指定的比较器来维护TreeMap的元素顺序
    if (cpr != null) {
         // do while循环，查找key要插入的位置（也就是新节点的父节点是谁）
        do {
            // 记录上次循环的节点t
            parent = t;
            // 比较当前节点的key和新插入的key的大小
            cmp = cpr.compare(key, t. key);
             // 新插入的key小的话，则以当前节点的左孩子节点为新的比较节点
            if (cmp < 0)
                t = t.left;
            // 新插入的key大的话，则以当前节点的右孩子节点为新的比较节点
            else if (cmp > 0)
                t = t.right;
            else
          // 如果当前节点的key和新插入的key想的的话，则覆盖map的value，返回
                return t.setValue(value);
        // 只有当t为null，也就是没有要比较节点的时候，代表已经找到新节点要插入的位置
        } while (t != null);
    }
    else {
        // 如果比较器为空，则使用key作为比较器进行比较
        // 这里要求key不能为空，并且必须实现Comparable接口
        if (key == null)
            throw new NullPointerException();
        Comparable<? super K> k = (Comparable<? super K>) key;
        // 和上面一样，循环查找新节点要插入的位置
        do {
            parent = t;
            cmp = k.compareTo(t. key);
            if (cmp < 0)
                t = t. left;
            else if (cmp > 0)
                t = t. right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    // 找到新节点的父节点后，创建节点对象
    Entry<K,V> e = new Entry<K,V>(key, value, parent);
    // 如果新节点key的值小于父节点key的值，则插在父节点的左侧
    if (cmp < 0)
        parent.left = e;
    // 如果新节点key的值大于父节点key的值，则插在父节点的右侧
    else
        parent.right = e;
    // 插入新的节点后，为了保持红黑树平衡，对红黑树进行调整
    fixAfterInsertion(e);
    // map元素个数+1
    size++;
    modCount++;
    return null;
}
 

/** 新增节点后对红黑树的调整方法 */
private void fixAfterInsertion(Entry<K,V> x) {
    // 将新插入节点的颜色设置为红色
    x.color = RED;

    // while循环，保证新插入节点x不是根节点或者新插入节点x的父节点不是红色（这两种情况不需要调整）
    while (x != null && x != root && x.parent.color == RED) {
        // 如果新插入节点x的父节点是祖父节点的左孩子
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
            // 取得新插入节点x的叔叔节点
            Entry<K,V> y = rightOf(parentOf(parentOf(x)));
            // 如果新插入x的父节点是红色-------------------①
            if (colorOf(y) == RED) {
                // 将x的父节点设置为黑色
                setColor(parentOf(x), BLACK);
                // 将x的叔叔节点设置为黑色
                setColor(y, BLACK);
                // 将x的祖父节点设置为红色
                setColor(parentOf(parentOf(x)), RED);
                // 将x指向祖父节点，如果x的祖父节点的父节点是红色，按照上面的步奏继续循环
                x = parentOf(parentOf(x));
            } else {
                // 如果新插入x的叔叔节点是黑色或缺少，且x的父节点是祖父节点的右孩子-------------------②
                if (x == rightOf(parentOf(x))) {
                    // 左旋父节点
                    x = parentOf(x);
                    rotateLeft(x);
                }
                // 如果新插入x的叔叔节点是黑色或缺少，且x的父节点是祖父节点的左孩子-------------------③
                // 将x的父节点设置为黑色
                setColor(parentOf(x), BLACK);
                // 将x的祖父节点设置为红色
                setColor(parentOf(parentOf(x)), RED);
                // 右旋x的祖父节点
                rotateRight(parentOf(parentOf(x)));
            }
        } else { // 如果新插入节点x的父节点是祖父节点的右孩子，下面的步奏和上面的相似，只不过左旋右旋的区分，不在细讲
            Entry<K,V> y = leftOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else {
                if (x == leftOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateRight(x);
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateLeft(parentOf(parentOf(x)));
            }
        }
    }
    // 最后将根节点设置为黑色，不管当前是不是红色，反正根节点必须是黑色
    root.color = BLACK;
}

/**
 * 对红黑树的节点(x)进行左旋转
 *
 * 左旋示意图(对节点x进行左旋)：
 *      px                              px
 *     /                               /
 *    x                               y               
 *   /  \      --(左旋)--             / \                
 *  lx   y                          x  ry    
 *     /   \                       /  \
 *    ly   ry                     lx  ly 
 *
 */
private void rotateLeft(Entry<K,V> p) {
    if (p != null) {
        // 取得要选择节点p的右孩子
        Entry<K,V> r = p.right;
        // "p"和"r的左孩子"的相互指向...
        // 将"r的左孩子"设为"p的右孩子"
        p.right = r.left;
        // 如果r的左孩子非空，将"p"设为"r的左孩子的父亲"
        if (r.left != null)
            r.left.parent = p;
        
        // "p的父亲"和"r"的相互指向...
        // 将"p的父亲"设为"y的父亲"
        r.parent = p.parent;
        // 如果"p的父亲"是空节点，则将r设为根节点
        if (p.parent == null)
            root = r;
        // 如果p是它父节点的左孩子，则将r设为"p的父节点的左孩子"
        else if (p.parent.left == p)
            p.parent.left = r;
        else
            // 如果p是它父节点的左孩子，则将r设为"p的父节点的左孩子"
            p.parent.right = r;
        // "p"和"r"的相互指向...
        // 将"p"设为"r的左孩子"
        r.left = p;
        // 将"p的父节点"设为"r"
        p.parent = r;
    }
}

   
/**
 * 对红黑树的节点进行右旋转
 *
 * 右旋示意图(对节点y进行右旋)：
 *            py                               py
 *           /                                /
 *          y                                x                 
 *         /  \      --(右旋)--             /  \                     
 *        x   ry                           lx   y 
 *       / \                                   / \                   
 *      lx  rx                                rx  ry
 *
 */
private void rotateRight(Entry<K,V> p) {
    if (p != null) {
        // 取得要选择节点p的左孩子
        Entry<K,V> l = p.left;
        // 将"l的右孩子"设为"p的左孩子"
        p.left = l.right;
        // 如果"l的右孩子"不为空的话，将"p"设为"l的右孩子的父亲"
        if (l.right != null) l.right.parent = p;
        // 将"p的父亲"设为"l的父亲"
        l.parent = p.parent;
        // 如果"p的父亲"是空节点，则将l设为根节点
        if (p.parent == null)
            root = l;
        // 如果p是它父节点的右孩子，则将l设为"p的父节点的右孩子"
        else if (p.parent.right == p)
            p.parent.right = l;
        //如果p是它父节点的左孩子，将l设为"p的父节点的左孩子"
        else p.parent.left = l;
        // 将"p"设为"l的右孩子"
        l.right = p;
        // 将"l"设为"p父节点"
        p.parent = l;
    }
}

红黑树的删除原理及TreeMap的remove实现

TODO