BloomFilter详解

什么是Bloom Filter

Bloom Filter是一种空间效率很高的随机数据结构，它的原理是，当一个元素被加入集合时，通过K个Hash函数将这个元素映射成一个位阵列（Bit array）中的K个点，把它们置为1。检索时，我们只要看看这些点是不是都是1就（大约）知道集合中有没有它了：如果这些点有任何一个0，则被检索元素一定不在；如果都是1，则被检索元素很可能在。这就是布隆过滤器的基本思想。

但Bloom Filter的这种高效是有一定代价的：在判断一个元素是否属于某个集合时，有可能会把不属于这个集合的元素误认为属于这个集合（false positive）。因此，Bloom Filter不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下，Bloom Filter通过极少的错误换取了存储空间的极大节省。

Bloom Filter示例图：

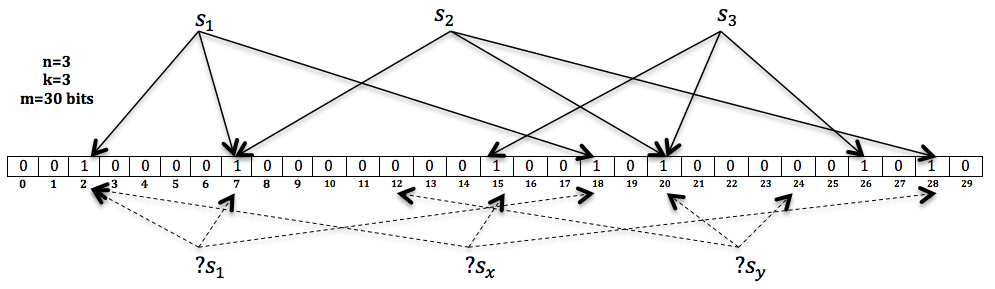
在这个示例中, 我们的Bloom Filter由一个30 bits的Bit Vector以及3个Hash Functions来构成。 我们将三个元素$S_1$, $S_2$和$S_3$分别插入这个Bloom Filter中。 然后对另外三个新元素$S_1$, $S_x$和$S_y$进行查询。 由图所示, $S_1$和$S_x$将被认为属于这个Bloom Filter, 因为所以相应的bit位均为1, 而$S_y$则被视为不属于这个Bloom Filter。 但是, 其中$S_x$为一个false positive的答案, 因为在插入的时候我们并没有插入这个元素。False Positive的答案是由Hash Collision造成的。我们可以根据要插入的元素的个数来变化BF的长度，从而减少误判率。

Bloom Filter主要参数计算

这部分涉及数学推理，不感兴趣的同学可以直接跳过记住结论。

影响Bloom Filter的性能的参数主要有四个:

• n : 需要插入Bloom Filter的最多的元素的个数
• m : Bloom Filter中bit位的个数
• k : Hash Functions的个数
• p : Bloom Filter的False Positive rate

其中需要插入Bloom Filter的最多元素的个数n我们是知道的, 或者至少是大致可以估算的。 所以构建一个Bloom Filter的时候, 主要需要设定bit位的个数, 从而来限制false positive rate的大小。 或者控制false positive rate的大小在一个固定值, 从而推算Bloom Filter的bit位的长度。

我们首先来看一个引理：

Lemma 1

用k个Hash Functions, 将n个元素插入到一个m bits的Bloom Filter中, 则这个Bloom Filter的任意一个bit位为0的概率将不会大于$e^{−\frac{k*n}{m}}$

这个Lemma计算Bloom Filter中任意一个bit位为0的概率。

证明：
用一个Hash Function插入一个元素后，某个特定bit位为0的概率为：$1 - \frac 1 m$
所以，用k个Hash Functions插入一个元素后，某个特定bit位为0的概率为：$\left(1 - {\frac 1 m}\right)^{kn}$
并且：
$$\lim_{m\to \infty}{\left(1 - {\frac 1 m}\right)^{kn}} = e^{−\frac{kn}{m}}$$

Lemma 2

假设我们运用Simple Uniform Hashing Functions对Bloom Filter进行插入操作，则这个Bloom Filter的False Positive率p是m，n和k的函数，并且$p = \left(1 - e^{−\frac{kn}{m}}\right)^k$

证明：
Simple Uniform Hashing函数会将每一个元素以相等的概率hash去m个bit位中的一个。当用一个确定的hash函数处理一个确定的元素，某个特定的bit位$b_x$没有被设置为1的概率为：$1 - {\frac 1 m}$
所以，当用k个Hash Function来处理这个元素的时候，某个特定的bit位$b_x$没有被设置为1的概率为：$\left(1 - {\frac 1 m}\right)^k$
然后，当用k个Hash Function来处理n个元素的时候，某个特定的bit位$b_x$没有被设置为1的概率为：$\left(1 - {\frac 1 m}\right)^{kn}$
相反，这个bit位被设置为1的概率为：$1 - \left(1 - {\frac 1 m}\right)^{kn}$

在查询阶段，如果这个元素在Bloom Filter中对应的的所有hash bits都被设置为了1，则这个元素被认为存在于查询集中。所以False Positive的概率为：$p = \left(1 - \left(1 - {\frac 1 m}\right)^{kn}\right)^k$

鉴于
$$\lim_{x\to 0}{\left(1 + x\right)^{\frac 1 x}} = e$$
$$\lim_{m\to \infty}{\left(-\frac 1 m\right)} = 0$$
$$\Rightarrow \lim_{m\to \infty}{\left(1 - \left(1 - {\frac 1 m}\right)^{kn}\right)^k} = \lim_{m\to \infty}{\left(1 - \left(1 - {\frac 1 m}\right)^{-m\times{\frac {-kn} m}}\right)^k} = \left(1 - e^{-\frac {nk} m}\right)^k$$

Lemma 3

假设我们用k个hash functions将n个元素插入到一个含有m个bit位的Bloom Filter中，则非0bit位的个数的期望值是：$m\cdot(1-e^{\frac{-kn}{m}})$

证明：
假设$X_j$是一组随机变量的集合，并且当第j个bit位为0的时候$X_j$=1，反之$X_j$为0。则，根据Lemma 2， $E\left[X_j\right] = (1-\frac{1}{m})^{kn} \approx e^{\frac{-kn}{m}}$

假设X为一个代表仍然为0的bit位的个数的随机变量，则：$E\left[X\right] = E\left[\sum_{i=1}^{m} X_i\right] = \sum_{i=1}^{m} E\left[X_i\right] \approx me^{\frac{-kn}{m}} $

所以非0bit位的个数的期望为：$m\cdot(1-e^{\frac{-kn}{m}})$

增加一个Bloom Filter的bit位的个数，可以减少发生Hash Collisions的几率，从而减少False Positive的概率。但是Bloom Filter的位数越多，它所占的硬盘空间就越大。在这里，我们假设，如果一个Bloom Filter一半的bit位被重置为1，则这个Bloom Filter达到了空间和Hash Collisions的平衡（当然这里你可以做其他假设）。 在这个假设前提下，我们可以来计算Bloom Filter主要参数之间的关系。

假设当一个Bloom Filter达到平衡状态的时候它含有n个元素，则下面这个方程描述了这个Bloom Filter的bit位的个数，与使用的hash function的个数及插入的元素个数之间的关系：$m = \frac{k \cdot n}{50\%} = 2 \cdot k \cdot n $ bits

Lemma 4

当$e^{-\frac{nk}{m}} = \frac{1}{2}$时， False Positive概率p达到最小值。此时：$k = ln2 \times \frac{m}{n}$， $p = \frac{1}{2}^k = 2^{-ln2 \times \frac{m}{n}}$

证明：
根据Lemma 2，$p = (1-e^{-\frac{nk}{m}})^k$
所以，p可以被认为是k的一个函数：$p = f(k) = (1-e^{-\frac{nk}{m}})^k$

则：$f(k) = (1 - b^{-k})^k$，$b = e^{-\frac{n}{m}}$ （1）
对方程（1）两边取log值，可以得到：$ln[ f(k)] = k \cdot ln(1-b^{-k})$ （2）
对方程（2）两边求导，可以得到：$\frac{1}{f(x)} \cdot f’(x) = ln(1-b^{-k}) + k \cdot \frac{1}{1-b^{-k}} \cdot (-1) \cdot (-b^{-k}) \cdot ln(b) = ln(1-b^{-k}) + k \cdot \frac{b^{-k} \cdot ln(b)}{1-b^{-k}}$ （3）
当方程（3）等于0的时候，方程（2）达到最小值。这时可以得到：$ln(1-b^{-k}) + k \cdot \frac{b^{-k} \cdot ln(b)}{1 - b^{-k}} = 0$ （4）
有：$(1- b^{-k}) \cdot ln(1- b^{-k}) = b^{-k} \cdot ln(b^{-k})$ （5）
根据方程（5）两边的对称性，可以得到：${1 - b^{-k}} = b^{-k}$ （6）
那么：$e^{-\frac{kn}{m}} = \frac{1}{2}$ （7）
可得：$k = ln2 \cdot \frac{m}{n}$ （8）
所以：$p = f(k) = (1-\frac{1}{2})^{k} = (\frac{1}{2})^k = 2 ^ {ln2 \cdot \frac{m}{n}}$

由Lemma 4可以推出以下定理：

已知一个Bloom Filter的False Positive为p，以及最多需插入元素的个数为n，则这个Bloom Filter的长度应为：
$$m = - \frac{n \cdot lnp}{(ln2)^2}$$
需用到的Hash Function的个数应为：
$$k = ln2 \cdot \frac{m}{n} = log_2\frac{1}{p}$$

Bloom Filter应用实例

Bloom-Filter一般用于在大数据量的集合中判定某元素是否存在。例如邮件服务器中的垃圾邮件过滤器。在搜索引擎领域，Bloom-Filter最常用于网络蜘蛛(Spider)的URL过滤，网络蜘蛛通常有一个URL列表，保存着将要下载和已经下载的网页的URL，网络蜘蛛下载了一个网页，从网页中提取到新的URL后，需要判断该URL是否已经存在于列表中。此时，Bloom-Filter算法是最好的选择。

Key-Value加快查询

一般Bloom-Filter可以与一些key-value的数据库一起使用，来加快查询。

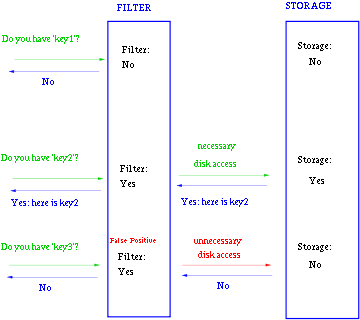
通常key-value存储系统的values存在硬盘，查询就是件费时的事。将Storage的数据都插入Filter，在Filter中查询都不存在时，那就不需要去Storage查询了。当False Position出现时，只是会导致一次多余的Storage查询。

由于Bloom-Filter所用的空间非常小，所有BF可以常驻内存。这样子的话，对于大部分不存在的元素，我们只需要访问内存中的Bloom-Filter就可以判断出来了，只有一小部分，我们需要访问在硬盘上的key-value数据库。从而大大地提高了效率。如图：

网络应用

1. P2P网络中查找资源操作，可以对每条网络通路保存Bloom Filter，当命中时，则选择该通路访问。
2. 广播消息时，可以检测某个IP是否已发包。
3. 检测广播消息包的环路，将Bloom Filter保存在包里，每个节点将自己添加入Bloom Filter。
4. 信息队列管理，使用Counter Bloom Filter管理信息流量。

垃圾邮件地址过滤

像网易，QQ这样的公众电子邮件（email）提供商，总是需要过滤来自发送垃圾邮件的人（spamer）的垃圾邮件。

一个办法就是记录下那些发垃圾邮件的email地址。由于那些发送者不停地在注册新的地址，全世界少说也有几十亿个发垃圾邮件的地址，将他们都存起来则需要大量的网络服务器。

如果用哈希表，每存储一亿个email地址，就需要1.6GB的内存（用哈希表实现的具体办法是将每一个email地址对应成一个八字节的信息指纹，然后将这些信息指纹存入哈希表，由于哈希表的存储效率一般只有50%，因此一个email地址需要占用十六个字节。一亿个地址大约要1.6GB，即十六亿字节的内存）。因此存贮几十亿个邮件地址可能需要上百GB的内存。

而Bloom Filter只需要哈希表1/8到1/4 的大小就能解决同样的问题。

BloomFilter决不会漏掉任何一个在黑名单中的可疑地址。而至于误判问题，常见的补救办法是在建立一个小的白名单，存储那些可能别误判的邮件地址。

线程安全性

在工作中使用了改进Guava的BloomFilter时，遇到了线程安全性的问题，在此记录一下自己的思考。

多线程读

在不存在写请求时，BloomFilter是一个静态的数据结构，此时每个bit位的0-1都不会被改变，所以多线程读是线程安全的。

多线程写

在并发写请求到来时，本质上每个写请求都是将BloomFilter的某几位置为1，《深入Java虚拟机》中对于线程安全的定义如下：

当多个线程访问同一个对象时，如果不用考虑这些线程在运行时环境下的调度和交替运行，也不需要进行额外的同步，或者在调用方进行任何其他的协调操作，调用这个对象的行为都可以获取正确的结果，那这个对象是线程安全的。

可见在多线程写的过程中，BloomFilter是非线程安全的，这是由于各个写线程调度情况未知，我们无法预测在写过程中BloomFilter每一位的状态。但对于多线程写，BloomFilter是最终线程安全的，也即当所有写请求处理完，生成的BloomFilter的状态是唯一的。

多线程读写

无需多言，多线程读写必然是非线程安全的。

由此我们可以得出一个结论，BloomFilter是非线程安全的。Guava在早些版本的BloomFilter也是非线程安全的，但在Guava Release 23后，社区推出了BloomFilter的线程安全特性。在该版本的commit中，我们可以看到改进后的BloomFilter是通过AtomicLongArray原子数组的方式保证线程一致性的，而早现版本的bitArray则是一个普通的long数组，故而有线程安全问题。

参考Bloom Filter详解、海量数据处理之Bloom Filter详解。